Content Start
A teacher asks students to find how many hours there are in 13 days. After some consideration, a student raises his hand and says the answer is 312. The teacher then asks, “How did you end up with 312?” Without much thought, the student responds, “Well, it just came to me.” The teacher tries again to get a better answer from the student but, to no avail, writes “13 x 24 = 312” on the board and moves to the next problem.
Many of us who have taught math might have encountered similar scenarios during our lessons. We eagerly want our students to be able to explain their thinking, yet, oftentimes, they seem stuck or are at a loss for words, and we don’t know how to proceed. We might ask our math coach for help. If you were the coach in this situation, what would you need to know to help this teacher?
Coaching is a complex endeavor that blends a myriad of concepts and skills. Practical experience, as well as content and coaching knowledge, are instrumental to becoming an effective math coach. We are going to start this series by looking at the content knowledge that is needed to teach mathematics effectively before we discuss how that content knowledge can connect to coaching knowledge to help teachers—such as the one in our example above—make better instructional decisions that maximize students’ learning of mathematics.
Mathematical Knowledge for Teaching
Mathematics is an old and multifaceted discipline, and there are many ways to conceptualize how mathematical content knowledge can be taught to others. For example, think about how you learned multiplication. Perhaps you started with physical manipulatives or by doing skip counting. Or perhaps you started with the number line or an array model. Maybe you memorized multiplication facts or used multiplication tables and never really used manipulatives. Any of these strategies can be used to teach multiplication, and a teacher needs to know not only what strategy to use but also why and when to use it.
 These kinds of instructional decisions highlight the demands math teachers are responding to every day as they consider the mathematics content to be taught, the level of mathematical understanding their students are capable of, and the best way to introduce the mathematical content in a lesson. Under these circumstances, the knowledge of mathematics needed for teaching is actually more, not less, than what the average person might need daily.
These kinds of instructional decisions highlight the demands math teachers are responding to every day as they consider the mathematics content to be taught, the level of mathematical understanding their students are capable of, and the best way to introduce the mathematical content in a lesson. Under these circumstances, the knowledge of mathematics needed for teaching is actually more, not less, than what the average person might need daily.
A good framework for thinking about the content knowledge teachers need to make instructional decisions is the Mathematical Knowledge for Teaching or MKT (Ball et al., 2008). In the MKT framework, knowledge of teaching is divided into the following parts:
Subject Matter Knowledge, with three subdivisions (Ball et al., 2008):
- Common Content Knowledge: Mathematical knowledge that is not necessarily unique to teaching but may be used in other settings (e.g., while shopping).
- Specialized Content Knowledge: Mathematical knowledge necessary and unique to teaching and that, as a rule, does not occur outside teaching (e.g., knowing the side-angle-side rule when proving congruency).
- Knowledge at the Mathematical Horizon: Knowledge of how mathematical topics are related over time, placing current content within the larger mathematical landscape to be taught (e.g., knowing how learning fraction arithmetic will help with learning algebra).
Pedagogical Content Knowledge, also with three subdivisions (Ball et al., 2008):
- Knowledge of Content and Students: Knowing students and their current understanding of mathematics, including misconceptions about content.
- Knowledge of Content and Teaching: Knowing the mathematics behind content and issues that might come up when presenting content to students.
- Knowledge of Curriculum: Specific knowledge regarding the school curriculum, including where content fits within a sequence of lessons or units.
Here’s a figure showing how these parts fit together (Hill & Ball, 2009):
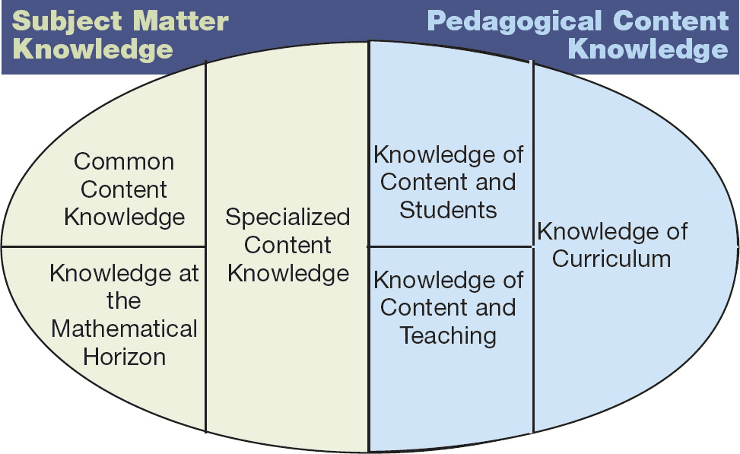
This is all great, but what does MKT have to do with coaching? For starters, MKT helps us describe the depth of content knowledge needed to be an effective math teacher. Look back at the figure—that’s a lot of knowledge! If anything, it is a humbling reminder that teaching mathematics at any grade level is no easy task.
Secondly, MKT can help us recognize holes in teachers’ knowledge base where they might need support. As a math coach, it is not a simple matter of telling a teacher, “You did it wrong. Here’s what you need to do.” That kind of advice is not helpful in the long run because it doesn’t let the teacher identify the root of the problem and thus be able to self-correct in the future.
Finally, MKT has been around for a while, and there is an available body of evidence about it that could be used to support teachers (Hilton & Hilton, 2019; Pincheira & Alsina, 2021; Spitzer & Phelps-Gregory, 2023). Although MKT is not the only way to conceptualize the content knowledge needed for teaching mathematics (Scheiner et al., 2017), it is a useful one and fits nicely with the knowledge of coaching we’ll discuss next.
Let’s review what we’ve covered so far:
- Math coaching is a complex endeavor, and to become an effective math coach, one has to blend practical experience with content and coaching knowledge.
- To help teachers make better instructional decisions, math coaches need to be aware of the different kinds of content knowledge teachers need in their line of work.
- MKT is a framework that can help us conceptualize the content knowledge for teaching mathematics that teachers need to be effective.
In our next post, we’ll see how content knowledge—as described in MKT—connects to coaching knowledge to help math teachers make better instructional decisions. Stay tuned!
Author: Guillermo Farfan, PhD, Region 7 Comprehensive Center
The contents of this blog series stem from a 2021 R7CC resource titled Considerations for Developing Effective Math Coaches: A Content-Driven Perspective, which can be accessed here.
References
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407. https://doi.org/10.1177/0022487108324554
Hill, H., & Ball, D. L. (2009). The curious—and crucial—case of mathematical knowledge for teaching. Phi Delta Kappan, 91(2), 68–71. https://doi.org/10.1177/003172170909100215
Hilton, A., & Hilton, G. (2019). Primary school teachers implementing structured mathematics interventions to promote their mathematics knowledge for teaching proportional reasoning. Journal of Mathematics Teacher Education, 22, 545–574. https://doi.org/10.1007/s10857-018-9405-7
Lasserre-Cortez, S., Cox, P., Goertzen, H., Jetty, L., Molina, C., & Vandeborne, L. (2021). Considerations for Developing Effective Math Coaches: A Content-Driven Perspective. Region 7 Comprehensive Center.
Pincheira, N., & Alsina, Á. (2021). Teachers’ mathematics knowledge for teaching early algebra: A systematic review from the MKT perspective. Mathematics, 9, 2590. https://doi.org/10.3390/math9202590
Scheiner, T., Montes, M. A., Godino, J. D., Carrillo, J., & Pino-Fan, L. R. (2017). What makes mathematics teacher knowledge specialized? Offering alternative views. International Journal of Science and Mathematics Education,17, 153–172. https://doi.org/10.1007/s10763-017-9859-6
Spitzer, S. M., & Phelps-Gregory, C. M. (2023). The relationship between prospective teachers’ mathematics knowledge for teaching and their ability to notice student thinking. Mathematics Education Research Journal. https://doi.org/10.1007/s13394-023-00455-z


 This material is in the public domain. While permission to reprint is not necessary, publication should be cited. This website was funded through the Office of Elementary and Secondary Education (OESE) and developed by the Region 7 Comprehensive Center at RMC Research Corporation. (Award # S283B190023). This website contains resources that are provided for the reader's convenience. These materials may contain the views and recommendations of various subject matter experts as well as hypertext links, contact addresses, and websites to information created and maintained by other public and private organizations. The U.S. Department of Education does not control or guarantee the accuracy, relevance, timeliness, or completeness of any outside information included in these materials. The views expressed herein do not necessarily represent the positions or policies of the U.S. Department of Education. No official endorsement by the U.S. Department of Education of any product, commodity, service, enterprise, curriculum, or program of instruction mentioned in this document is intended or should be inferred.
This material is in the public domain. While permission to reprint is not necessary, publication should be cited. This website was funded through the Office of Elementary and Secondary Education (OESE) and developed by the Region 7 Comprehensive Center at RMC Research Corporation. (Award # S283B190023). This website contains resources that are provided for the reader's convenience. These materials may contain the views and recommendations of various subject matter experts as well as hypertext links, contact addresses, and websites to information created and maintained by other public and private organizations. The U.S. Department of Education does not control or guarantee the accuracy, relevance, timeliness, or completeness of any outside information included in these materials. The views expressed herein do not necessarily represent the positions or policies of the U.S. Department of Education. No official endorsement by the U.S. Department of Education of any product, commodity, service, enterprise, curriculum, or program of instruction mentioned in this document is intended or should be inferred.