Content Start
Recall that we started our series by looking at a scenario where a teacher asks a student repeatedly to explain how he got his answer, but the student is not able to express anything other than, “It just came to me.” Later, the teacher comes to a math coach for help—how should the situation be handled in the future if students aren’t able to explain their thinking?
We previously saw that, to begin answering that question, we needed to look at the content knowledge that is needed to teach mathematics effectively. An effective math coach would master many skills, but the foundation must be content expertise. Just as teachers cannot teach what they do not know, math coaches cannot coach teachers without having content knowledge expertise to identify pedagogical, instructional, and assessment needs. In Part 1, we identified the Mathematical Knowledge for Teaching, or MKT, as a good framework to help us think about math content knowledge in a classroom setting (Hill & Ball, 2009).
We are now going to discuss how MKT can connect to coaching knowledge (i.e., knowledge specifically about coaching others) to help math teachers—such as the one in our scenario above—make better instructional decisions that maximize students’ learning of mathematics.
 Coaching Knowledge in Mathematics
Coaching Knowledge in Mathematics
To begin with, what does coaching knowledge in mathematics look like? This is a difficult question to answer from scratch; thankfully, researchers working on a five-year project known as Examining Mathematics Coaching (EMC) have identified the following eight domains that describe the kinds of knowledge math coaches need when helping math teachers (Sutton et al., 2011):
- Assessment
- Communication
- Leadership
- Relationships
- Student Learning
- Teacher Development
- Teacher Learning
- Teacher Practice
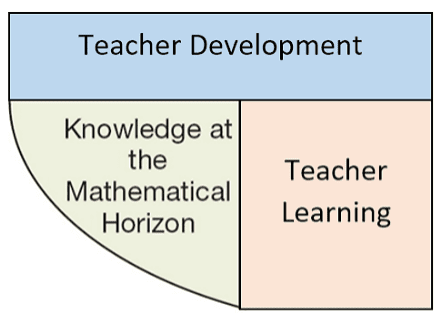
Much of what is included in these eight domains aligns with the National Council of Teachers of Mathematics (NCTM) guiding principles of effective mathematics programs (NCTM, 2014). In this blog post, we will focus on the last three domains—Teacher Development, Learning, and Practice—and how these connect back to MKT, leaving the remaining five domains for a future post.
 Teacher Development, Learning, and Practice. The EMC defines the domain of Teacher Development as knowledge about “various models of teacher stages of development, adult change, and the continuum of learning that teachers experience,” including how to “diagnose where a teacher is, recognize potential learning trajectories, and differentiate strategies to support an individual teacher’s growth” (Sutton et al., 2011, p. 21). In other words, Teacher Development is how a math coach knows where on the spectrum from novice to expert a teacher is, as well as the motivations for and barriers to growth an individual teacher might have.
Teacher Development, Learning, and Practice. The EMC defines the domain of Teacher Development as knowledge about “various models of teacher stages of development, adult change, and the continuum of learning that teachers experience,” including how to “diagnose where a teacher is, recognize potential learning trajectories, and differentiate strategies to support an individual teacher’s growth” (Sutton et al., 2011, p. 21). In other words, Teacher Development is how a math coach knows where on the spectrum from novice to expert a teacher is, as well as the motivations for and barriers to growth an individual teacher might have.
The Teacher Learning domain is defined by the EMC as knowledge about “the myriad ways that teachers know and understand mathematics content,” including “teacher beliefs about learning” (Sutton et al., 2011, p. 21). This involves identifying how a teacher best learns mathematics content and recognizing the discrepancy between a teacher knowing a concept, strategy, or skill and effectively using that concept, strategy, or skill.
Finally, the Teacher Practice domain is defined as knowledge about “teacher beliefs [regarding] mathematics teaching practice” as well as knowledge of “instructional resources for effective management and mathematics learning” (Sutton et al., 2011, p. 21). These resources include lesson planning, school supports, models of instruction, assessment, etc. More importantly, an effective math coach will know how practices and resources translate into teacher actions in the mathematics classroom.
Now that we have dealt with the EMC domains of Teacher Development, Learning, and Practice in some detail, let’s illustrate how these domains intersect with MKT as math coaches help teachers become more effective in teaching mathematics using two examples.
1. Effective math coaches help teachers recognize connections between or among seemingly unrelated ideas.
In addition to being able to explain why a particular concept, strategy, or skill in mathematics is true or why it is worth knowing, teachers must be able to show how a concept, strategy, or skill relates to other ideas, both within a lesson and between lessons. For instance, let’s look at what happens when one uses concrete area models to solve 4 x 23.
A novice teacher, following the traditional presentation of area models, will probably break “23” into 20 and 3 and do an area model with partial products like below:
 (4 x 20) + (4 x 3) = 80 + 12 = 92
(4 x 20) + (4 x 3) = 80 + 12 = 92
This is mathematically correct; however, an effective math coach will help this teacher recognize that if one groups ten single units to form another block of ten, you end up with nine sets of ten and two ones, and the resulting model will look like this:
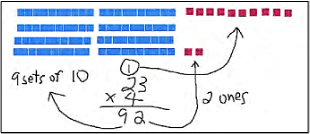
(9 x 10) + 2 = 90 + 2 = 92
This second area model visually connects what happens when you use the standard algorithm to answer 4 x 23: as you multiply “4 x 3” under the ones column, you write down “2” ones and write “1” at the top of the tens column. Next, you do “4 x 2” under the tens column and add the previous “1” to obtain “9” tens. You’ve effectively reversed the explanation of the second area model and got the same answer: 92!
Showing this alternative way of multiplying 4 x 23 using an area model connects students’ concrete understanding of operations using tens and ones blocks with the abstract concept of an algorithm (MKT: Knowledge at the Mathematical Horizon). That’s no small feat! Many students struggle with the standard algorithm precisely because it requires moving from the concrete to the abstract, and the first area model we saw offers no help in bridging that gap. An effective math coach will identify not only if a teacher knows area model multiplication but also if the teacher knows how to extend the area model to make connections to other concepts (EMC: Teacher Development & Learning).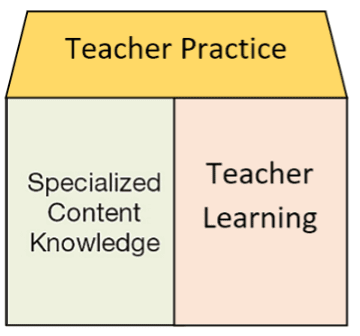
2. Effective math coaches help teachers understand that the bulk of fundamental mathematics involves taking things apart, putting things together, or rearranging them.
Most mathematics, particularly at the elementary level, consists of recognizing the “building blocks” underlying simple operations with mathematical objects (e.g., numbers, shapes) and how bigger mathematical structures effectively “rest on” a good understanding of those building blocks.
A good example is finding the area of an irregular polygon. One learns quickly that students often have an easier time finding the area for Figure A than the area for Figure B:
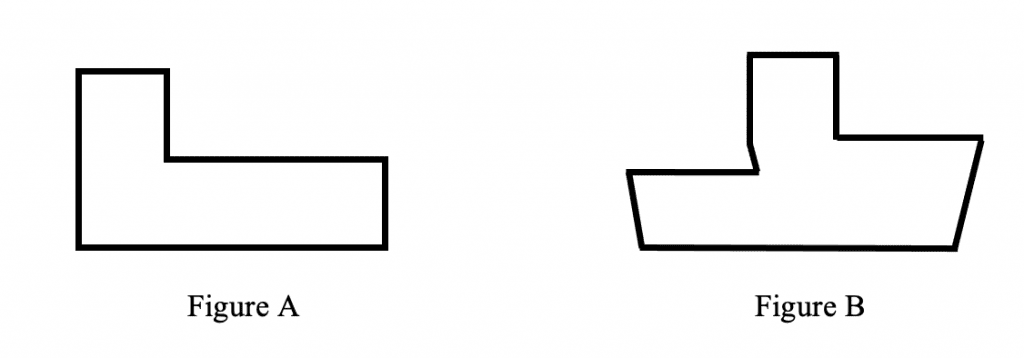
A teacher might mistakenly think students struggling with Figure B only need to practice more with tiled shapes or memorize the formulas for areas to be able to find the answer. However, an effective math coach will point out instead that the issue might be more basic: Students often don’t know how to partition complex figures into simpler ones with familiar areas (MKT: Specialized Content Knowledge). Merely practicing with tiled shapes or memorizing area formulas will hardly be enough to overcome this difficulty. It is only when students begin to understand that any two-dimensional polygon can be broken into any number of smaller polygons that a way forward can be found.
So, how should a teacher use Figure B to help students realize that? An effective math coach could ask the teacher to activate students’ prior knowledge of shapes that have easy-to-calculate areas, such as the square, rectangle, triangle, and trapezoid, by providing students with a worksheet of said shapes and their area formulas. With this knowledge, students will then be asked to partition Figure B into any combination of these four shapes that will make it easier to calculate the total area. And here’s the rub: there are multiple ways you could partition Figure B! Letting students practice partitioning Figure B into any of the four shapes they already know is a good way to stimulate their understanding of the geometry and areas of irregular polygons.
Let’s say that students come up with four possible combinations:
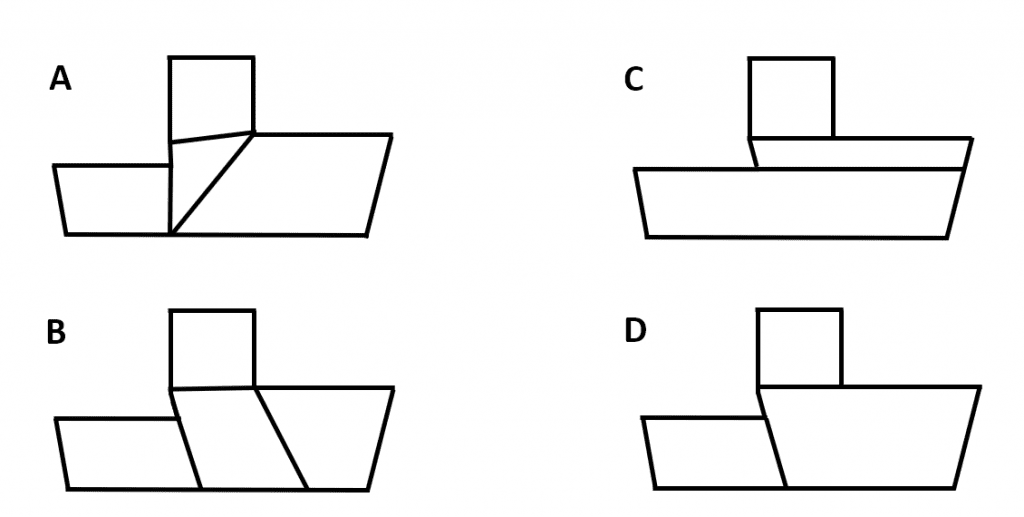
The math coach will emphasize that the point of the exercise is not merely to partition Figure B using squares, rectangles, triangles, and/or trapezoids, but to partition Figure B in a way that will make it easier (not harder) to find the total area. Although, technically, all four combinations could be used to find the area of the irregular polygon, option D appears the most clean and straightforward. A teacher could then ask students to find the total area using each of the combinations and compare which of the four was indeed the easiest.
An effective math coach will identify if a teacher knows how to use questions students often find difficult as opportunities to not only tap into students’ prior knowledge of more basic concepts but also utilize resources that use that knowledge to solve more challenging problems (EMC: Teacher Practice & Learning).
Let us sum up what we’ve learned in this post by looking at the following highlights:
- According to Sutton et al. (2011), coaching knowledge in mathematics consists of eight domains: Assessment, Communication, Leadership, Relationships, Student Learning, Teacher Development, Teacher Learning, and Teacher Practice.
- The domains of Teacher Development, Learning, and Practice all deal with the teacher as a person: where they are in terms of growth, how they learn mathematical content, and how well they use resources to stimulate students’ understanding during lessons.
- We saw two examples of how these three domains of coaching knowledge intersect with MKT during a mathematics lesson.
In our next post, we’ll cover how the other domains of coaching knowledge also intersect with MKT to help math coaches assist teachers in making better instructional decisions. Stay tuned!
Author: Guillermo Farfan, PhD, Region 7 Comprehensive Center
The contents of this blog series stem from a 2021 R7CC resource titled Considerations for Developing Effective Math Coaches: A Content-Driven Perspective, which can be accessed here.
References
Hill, H., & Ball, D. L. (2009). The curious—and crucial—case of mathematical knowledge for teaching. Phi Delta Kappan, 91(2), 68–71. https://doi.org/10.1177/003172170909100215
Lasserre-Cortez, S., Cox, P., Goertzen, H., Jetty, L., Molina, C., & Vandeborne, L. (2021). Considerations for Developing Effective Math Coaches: A Content-Driven Perspective. Region 7 Comprehensive Center.
National Council of Teachers of Mathematics. (2014). Principles to actions executive summary. https://www.nctm.org/uploadedFiles/Standards_and_Positions/PtAExecutiveSummary.pdf
Sutton, J. T., Burroughs, E. A., & Yopp, D. A. (2011). Coaching knowledge: Domains and definitions. Journal of Mathematics Education Leadership, 13(2), 12–20. https://www.montana.edu/emc/documents/NCSM.Coaching.Knowledge.Fall2011.pdf


 This material is in the public domain. While permission to reprint is not necessary, publication should be cited. This website was funded through the Office of Elementary and Secondary Education (OESE) and developed by the Region 7 Comprehensive Center at RMC Research Corporation. (Award # S283B190023). This website contains resources that are provided for the reader's convenience. These materials may contain the views and recommendations of various subject matter experts as well as hypertext links, contact addresses, and websites to information created and maintained by other public and private organizations. The U.S. Department of Education does not control or guarantee the accuracy, relevance, timeliness, or completeness of any outside information included in these materials. The views expressed herein do not necessarily represent the positions or policies of the U.S. Department of Education. No official endorsement by the U.S. Department of Education of any product, commodity, service, enterprise, curriculum, or program of instruction mentioned in this document is intended or should be inferred.
This material is in the public domain. While permission to reprint is not necessary, publication should be cited. This website was funded through the Office of Elementary and Secondary Education (OESE) and developed by the Region 7 Comprehensive Center at RMC Research Corporation. (Award # S283B190023). This website contains resources that are provided for the reader's convenience. These materials may contain the views and recommendations of various subject matter experts as well as hypertext links, contact addresses, and websites to information created and maintained by other public and private organizations. The U.S. Department of Education does not control or guarantee the accuracy, relevance, timeliness, or completeness of any outside information included in these materials. The views expressed herein do not necessarily represent the positions or policies of the U.S. Department of Education. No official endorsement by the U.S. Department of Education of any product, commodity, service, enterprise, curriculum, or program of instruction mentioned in this document is intended or should be inferred.