Content Start
In our previous post, we saw how coaching knowledge in mathematics can be conceptualized as comprising eight domains (Sutton et al., 2011):
- Assessment
- Communication
- Leadership
- Relationships
- Student Learning
- Teacher Development
- Teacher Learning
- Teacher Practice
We described the last three domains of coaching knowledge—Teacher Development, Learning, and Practice—and saw two examples of how these domains intersect with Mathematical Knowledge for Teaching or MKT (Hill & Ball, 2009) to help math coaches assist teachers in making better instructional decisions.
Today we will focus on the remaining coaching knowledge domains and how these domains intersect with MKT in ways that could be useful to math coaches and their teachers.
Coaching Knowledge in Mathematics
To help teachers make informed decisions about improving instruction, math coaches often need data on students’ learning of mathematics. Hence, we’ll begin with the Examining Mathematics Coaching (EMC) research project’s domains of Assessment and Student Learning before passing to the domains of Communication, Leadership, and Relationships.
Assessment. The EMC defines the domain of Assessment as knowledge on how to both “diagnose teachers’ needs—personal, instructional, content, and management” as well as “determine what a teacher knows about assessment, including different types, uses, and limits” (Sutton et al., 2011, p. 19). This includes knowing how to set goals, evaluate lesson effectiveness, inspect student work, and interpret and use assessment data to adjust instruction and scaffold student learning.
Student Learning. The domain of Student Learning is defined by EMC as knowledge on how to “support teachers in acquiring facility with mathematical processes (mathematical discourse, mathematical exploration, meta-cognition, etc.) that help students engage in challenging and meaningful mathematics problems and tasks,” including how to “analyze student thinking and conduct mathematical error analysis” (Sutton et al., 2011, p. 20). This involves coaches being current on research on how students learn mathematics over time, translating said research in ways teachers can understand, and helping teachers recognize evidence of learning potential and deficits in student work.
Let us now see two examples of how the EMC domains of Assessment and Student Learning intersect with MKT as math coaches help teachers become more effective in teaching mathematics.
 3. Effective math coaches use their understanding of students’ learning of mathematics to develop teachers’ observation skills regarding student thinking.
3. Effective math coaches use their understanding of students’ learning of mathematics to develop teachers’ observation skills regarding student thinking.
Part of a teacher’s repertoire must include strategies to reveal what a student is thinking during their learning process. All too often, a teacher only has a jumble of written computation to judge how and why a student approached the solution to a problem. This is insufficient, and teachers typically have to resort to oral questioning to determine a student’s line of reasoning (EMT: Assessment).
Recall our original problem of asking how many hours are in 13 days. A student says the answer is 312, but when asked to explain how he got the answer, he only replies, “Well, it just came to me.” An effective math coach will suggest that the task include students writing down their thought processes, not just the answer, which would reveal information beyond the final solution (EMT: Student Learning).
However, there’s another problem we must address: many times, students don’t know how to write down their thought processes! Writing down one’s thoughts is not a skill we’re born with. We must learn how to do it. Oftentimes, teachers will have to translate students’ oral thinking to provide them with guidance on how to write their ideas mathematically. In this scenario, rather than marking the right answer and moving on, the math coach might suggest the teacher instead show how he would have solved the problem and then invite students to offer their solutions. As students provide their explanations, the teacher translates their thoughts into mathematical language everyone can follow. For example, a student might say, “I know there’s 24 hours in 1 day, and I multiplied 13 by 24.” Note that the student’s explanation is incomplete, as it does not mention how he got to multiply 13 by 24. In this case, the teacher might write the progression as follows:
1 day = 24 hours
13 x 1 day = 13 x 24 hours
13 days = 312 hours
Such an approach would reveal not only what the student knows about multiplication but also the implicit assumptions they made when solving the problem (MKT: Knowledge of Content and Students).
 4. Effective math coaches use their understanding of students’ learning of mathematics across multiple grade levels to help teachers recognize potential pitfalls during instruction.
4. Effective math coaches use their understanding of students’ learning of mathematics across multiple grade levels to help teachers recognize potential pitfalls during instruction.
Mathematics, particularly in the elementary grades, is a layered science: new concepts, strategies, and skills at one level are often built on ideas or content that were introduced at a previous level. However, as they respond to the day-to-day challenges of instructing in mathematics, teachers might lose sight of this point and become unaware of how their instruction might have adverse repercussions down the road (EMT: Assessment).
An effective math coach, on the other hand, should always keep in mind that the mathematics students are supposed to learn today will connect with the mathematics they will engage with in the future (MKT: Knowledge at the Mathematical Horizon). Having this broad, holistic perspective can thus let math coaches help teachers avoid certain pitfalls that could occur during instruction. Let us illustrate using the example of a three-digit addition problem: 247 + 531. To help students understand the steps involved, a teacher might find it useful to break down the addition into partial sums as below:
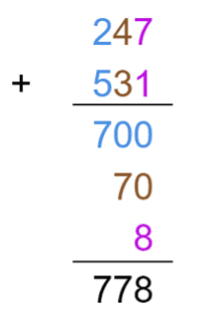 The teacher highlighted the partial sums according to place value: 200 + 500 (hundreds in blue), 40 + 30 (tens in brown), and 7 + 1 (ones in purple). This looks like a neat way to do a three-digit addition! However, notice that the pattern of the partial sums “slant” from left to right, which is contrary to what happens in later instruction when the standard algorithm for multiplication is introduced:
The teacher highlighted the partial sums according to place value: 200 + 500 (hundreds in blue), 40 + 30 (tens in brown), and 7 + 1 (ones in purple). This looks like a neat way to do a three-digit addition! However, notice that the pattern of the partial sums “slant” from left to right, which is contrary to what happens in later instruction when the standard algorithm for multiplication is introduced:
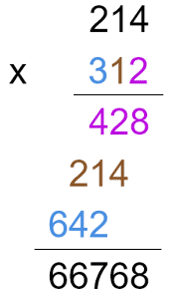
Here, the order is dictated by multiplying each of the digits in 312 with 214, starting from the ones place: 2 x 214 (ones in purple), 1 x 214 (tens in brown), and 3 x 214 (hundreds in blue). To account for place value, the partial products “slant” from right to left this time. Although we, as adults, might not see this as a significant issue, for students who learned three-digit sums one way and are just beginning to understand and use the standard algorithm for multiplying three-digit numbers the other way, it sure could be confusing (EMT: Student Learning)!
An effective math coach might suggest a better way to express the same idea of 247 + 531 with partial sums but in a way that avoids any future confusion with multiplication and still reinforces the idea of place value—we’ll call this the method of expanded notation:

This approach accomplishes the same goal as our first addition example while at the same time avoiding confusing students regarding place value when adding or multiplying three-digit numbers!
We’re now going to deal with the domains of Communication, Leadership, and Relationships and illustrate one last example of how these domains intersect with MKT as math coaches help teachers become more effective in teaching mathematics.
Communication. The EMC defines the domain of Communication as knowledge regarding “how to communicate professionally with others about students, curriculum, and classroom practice,” including “how to mediate a conversation, by pausing, paraphrasing, probing, and inquiring” (Sutton et al., 2011, p. 19). This involves asking reflective questions, using non-verbal communication, and listening actively during conversations.
Leadership. The domain of Leadership is defined by the EMC as the knowledge to “strategically identify, define, and communicate specific goals and objectives that relate to student success and teachers’ professional growth [that] align with the institution’s vision for mathematics” (Sutton et al., 2011, p. 19). This includes coaches using their leadership knowledge to work with other school leaders, bridge the gap that may exist between teachers’ beliefs and their ability to implement instruction that reflects those beliefs, earn teachers’ and administrators’ trust, and enhance teachers’ content knowledge.
Relationships. The EMC defines the domain of Relationships as the knowledge necessary to “establish and maintain rapport and credibility with teachers and other stakeholders based on trust, empathy, mutual understanding, and confidentiality,” including knowing “about environments where positive relationships take place” (Sutton et al., 2011, p. 20). This involves knowing how to work with people and the culture of specific districts and schools.
Now let’s look at one more example of the intersection between these domains of coaching knowledge and MKT.
 5. Effective math coaches understand the importance of conducting effective debriefs with teachers after classroom observations.
5. Effective math coaches understand the importance of conducting effective debriefs with teachers after classroom observations.
Real observations of classroom instruction should be an integral part of a math coach’s job. However, it is often easy for teachers (and coaches!) to focus on teaching strategies (how things are taught) rather than on the content (what was taught). An effective math coach will make a point to meet with teachers after classroom observations and address both teaching and content stemming from those observations (EMT: Leadership).
 A math coach should be skilled at asking probing questions during debriefs to discuss the impact of instructional practice, student learning, coaching support, and next steps (EMC: Communication). For example, if a teacher tells a math coach that students seem to do badly with mixed fractions, the coach must be prepared to successfully diagnose why students are struggling with mixed fractions and the extent of the teacher’s knowledge on the topic. In this situation, it would be key for the coach to gather student work and determine if the teacher knows of only one strategy to work with mixed fractions. A lack of expertise in fraction arithmetic could severely limit the alternative strategies a teacher could employ to help students understand the idea of mixed fractions (MKT: Specialized Content Knowledge). It is also important that, in communicating with the teacher, the math coach does not assign blame to either the teacher or the students but rather addresses content shortcomings tactfully (EMC: Relationships).
A math coach should be skilled at asking probing questions during debriefs to discuss the impact of instructional practice, student learning, coaching support, and next steps (EMC: Communication). For example, if a teacher tells a math coach that students seem to do badly with mixed fractions, the coach must be prepared to successfully diagnose why students are struggling with mixed fractions and the extent of the teacher’s knowledge on the topic. In this situation, it would be key for the coach to gather student work and determine if the teacher knows of only one strategy to work with mixed fractions. A lack of expertise in fraction arithmetic could severely limit the alternative strategies a teacher could employ to help students understand the idea of mixed fractions (MKT: Specialized Content Knowledge). It is also important that, in communicating with the teacher, the math coach does not assign blame to either the teacher or the students but rather addresses content shortcomings tactfully (EMC: Relationships).
Let us sum up what we’ve learned in this post by looking at the following highlights:
- The domains of Assessment and Student Learning deal with how to help teachers use data to understand students’ learning of mathematics, while the domains of Communication, Leadership, and Relationships deal with how math coaches interact with their colleagues and their sociocultural environments to enact effective math instruction.
- We saw several examples of how these domains of coaching knowledge intersect with MKT during different mathematics scenarios.
In our final post, we’ll discuss some final considerations math coaches should keep in mind when assisting teachers in making better instructional decisions. Stay tuned!
Author: Guillermo Farfan, PhD, Region 7 Comprehensive Center
The contents of this blog series stem from a 2021 R7CC resource titled Considerations for Developing Effective Math Coaches: A Content-Driven Perspective, which can be accessed here.
References
Hill, H., & Ball, D. L. (2009). The curious—and crucial—case of mathematical knowledge for teaching. Phi Delta Kappan, 91(2), 68–71. https://doi.org/10.1177/003172170909100215
Lasserre-Cortez, S., Cox, P., Goertzen, H., Jetty, L., Molina, C., & Vandeborne, L. (2021). Considerations for Developing Effective Math Coaches: A Content-Driven Perspective. Region 7 Comprehensive Center.
Sutton, J. T., Burroughs, E. A., & Yopp, D. A. (2011). Coaching knowledge: Domains and definitions. Journal of Mathematics Education Leadership, 13(2), 12–20. https://www.montana.edu/emc/documents/NCSM.Coaching.Knowledge.Fall2011.pdf

 3. Effective math coaches use their understanding of students’ learning of mathematics to develop teachers’ observation skills regarding student thinking.
3. Effective math coaches use their understanding of students’ learning of mathematics to develop teachers’ observation skills regarding student thinking. 4. Effective math coaches use their understanding of students’ learning of mathematics across multiple grade levels to help teachers recognize potential pitfalls during instruction.
4. Effective math coaches use their understanding of students’ learning of mathematics across multiple grade levels to help teachers recognize potential pitfalls during instruction. 5. Effective math coaches understand the importance of conducting effective debriefs with teachers after classroom observations.
5. Effective math coaches understand the importance of conducting effective debriefs with teachers after classroom observations.
 This material is in the public domain. While permission to reprint is not necessary, publication should be cited. This website was funded through the Office of Elementary and Secondary Education (OESE) and developed by the Region 7 Comprehensive Center at RMC Research Corporation. (Award # S283B190023). This website contains resources that are provided for the reader's convenience. These materials may contain the views and recommendations of various subject matter experts as well as hypertext links, contact addresses, and websites to information created and maintained by other public and private organizations. The U.S. Department of Education does not control or guarantee the accuracy, relevance, timeliness, or completeness of any outside information included in these materials. The views expressed herein do not necessarily represent the positions or policies of the U.S. Department of Education. No official endorsement by the U.S. Department of Education of any product, commodity, service, enterprise, curriculum, or program of instruction mentioned in this document is intended or should be inferred.
This material is in the public domain. While permission to reprint is not necessary, publication should be cited. This website was funded through the Office of Elementary and Secondary Education (OESE) and developed by the Region 7 Comprehensive Center at RMC Research Corporation. (Award # S283B190023). This website contains resources that are provided for the reader's convenience. These materials may contain the views and recommendations of various subject matter experts as well as hypertext links, contact addresses, and websites to information created and maintained by other public and private organizations. The U.S. Department of Education does not control or guarantee the accuracy, relevance, timeliness, or completeness of any outside information included in these materials. The views expressed herein do not necessarily represent the positions or policies of the U.S. Department of Education. No official endorsement by the U.S. Department of Education of any product, commodity, service, enterprise, curriculum, or program of instruction mentioned in this document is intended or should be inferred.